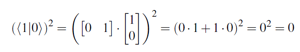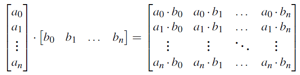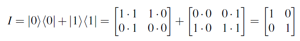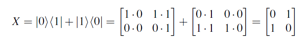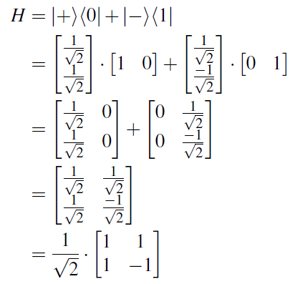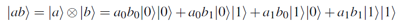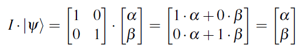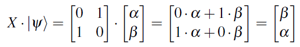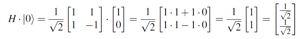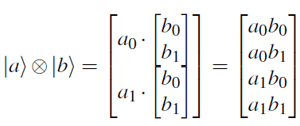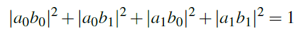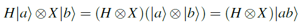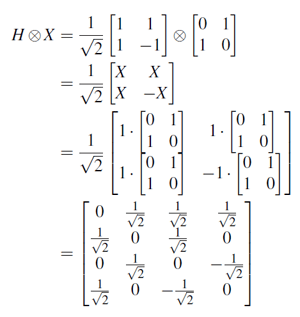Matrix Operations

Introduction to Quantum Computing

Matrix Operations

• Inner Product - vector multiplication that produces a scalar
  • results from multiplying a row vector with a column vector                  
  • <a|b> = [a0 a1 ... an ] x [ b0] = a1b0 + a1b1 + ... + anbn
                                                [ b1 ]
  • its square denotes the probability
  • use the inner product to obtain the probability amplitude of measuring a particular value from a qubit state bn
  • 
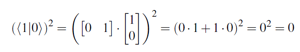
• Outer Product - vector multiplication that produces a matrix
  • results from multiplying a column vector multiplied by a row vector
  • |a><b| =
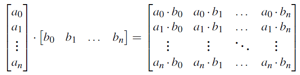
• Identity Matrix
  •  
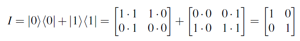
  • applying the I-gate results in unchanged vector
    • 
• Not (X) Matrix
  • 
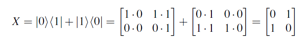
  • applying the X-gate flips the probability amplitudes
    • 
• Hadamard (H) Matrix 
  •  
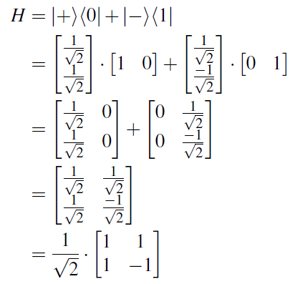
  • applying the Hadamard gate puts the basis state into superposition
    • 
• Tensor Product
  • the tensor product is represented as |a> ⊗ |b>
  • two qubits yield four combinations of the basis states
  • these form a quantum system of their own, so they can be represented by a single equation - |ab> where ab is just a name
  • 
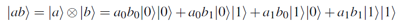
  • used to calculate the amplitudes and the amplitude squared must be 1
    • 
    • 
  • apply a H-gate and a X-gate
    • 
    •