Probability

Introduction to Quantum Computing

Probability

A numerical descriptions of how likely an event is to occur.  The higher the probability of an event, the more likely it is that the event will occur.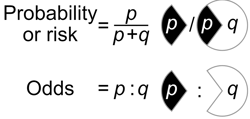

• marginal probability: the absolute probability of an event irrespective of any further information
• joint probability: the probability of two events occurring together; multiply both marginal probabilities to obtain the joint probability. Given that two random variables are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs
• conditional probability: the probability of one event given that another event occurred
• prior probability: the unconditional probability before any relevant evidence is taken into account
• posterior probability: the revised or updated probability of an event occurring after taking into consideration new information
  • the conditional probability P(A|B) of an event A given B

  • EXAMPLE: A school has 60% boys and 40% girls as students.  The girls wear trousers or skirts in equal numbers; all boys wear trousers.  An observer sees a student wearing trousers from a distance.

    • What is the probability this student is a girl?

      • P(G): the probability that the student is a girl regardless of any other information. The percentage of girls is 40% - this probability equals 0.4.
      • P(B): the probability that the student is a boy) regardless of any other information. B is the complementary event to G. This is 60%, or 0.6.
      • P(T|G): or the probability of the student wearing trousers given that the student is a girl. As they are as likely to wear skirts as trousers, this is 0.5.
      • P(T|B): or the probability of the student wearing trousers given that the student is a boy. This is given as 1.
      • P(T): or the probability of a (randomly selected) student wearing trousers regardless of any other information.
        P(T) = P(T|G) P(G) + P(T|B) P(B) via the law of total probability, this is ...
        P(T) = (0.5 * 0.4) + (1 * 0.6) = 0.8.

      • Given this information, the posterior probability of having spotted a girl given that the student is wearing trousers is computed by substituting the values in the formula. 
        The event G is that the student observed is a girl, and the event T is that the student observed is wearing trousers.

        P(Hypothesis|Evidence)=(P(Hypothes)*P(Evidence|Hypothes))/P(Evidence)
        posterior = prior * modifier
        P(G|T) = (P(G) * P(T|G)) / P(T) = (0.4 * 0.5) / 0.8 =0.25.