Grover's Algorithm / Search

Grover’s Algorithm for Efficient Search applies when you have a function which returns "True" for one of its possible inputs, and "False" for all the other inputs.  The algorithm is designed to find the one input that returns "True".

What the algorithm really does is it searches through the input of the function until it finds that single input that causes the function to return true.

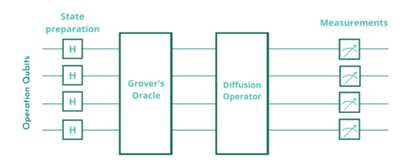
So, how does the algorithm work?  Grover's algorithm consists of three main steps: 1) state preparation, 2) the oracle, and 3) the diffusion operator.

Before starting, the location of the marked item is unknown. 

In the first step, the search space is created.  This search space consists of all the possible cases. Since any guess is as good as any other guess, the locations can be expressed in terms of a uniform superposition.  Note: if there are 3 qubits in the system, the list of all possible cases is the states |000> through |111>.  So, with 3 qubits, the size of the available search space or list can be, at most, N = 2³ = 8.

2. Oracle:

In the second step, the oracle marks the correct answer(s). The oracle adds a negative phase to the solution states so it will standout.   So, the oracle is a diagonal matrix with the entry that correspond to the marked item having a negative phase.

3. Diffusion Operator:

In the third step, the diffusion operator magnifies the answers so they stand out and can be measured.