What Is RSA Cryptography?

Introduction to Quantum Computing

RSA

The RSA algorithm involves four steps:

1. Key Generation (a public key 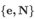and a private key ) 
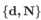2. Key Distribution,
3. Message Encryption
4. Message Decryption

Terms:

• m = plaintext message
• c = unreadable ciphertext
• e = Public Key
• d = private key
• N = large number which is the product of two prime numbers
• p = prime number
• q = prime number
• r = periodicity

Formulas:

• Modular Exponentiation
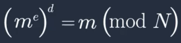
• Encrypted ciphertext
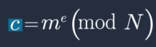
• Decrypt ciphertext
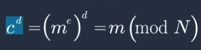
• Order finding
• choose e
• solve for d or de mod r = 1 

Example:

1. Key Generation
   1. choose prime numbers for "p" and "q" at random --- p = 2, q = 5
   2. calculate "N" = p * q --- N = 2 * 5 = 10
   3. determine "e" and "d" -- need to determine the periodicity property
   4. 
      (p-1)(q-1) / r = integer
      (2-1)(5-1) / 4 = 1*4 = 4
      this checks compared to the observed period "r"
   5. now, determine "e" and "d"
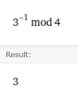
      first choose an "e" such that 3 <= e <= r
      1. e = 3
         d=3